Page 1: The Mod Operator

Unit 2, Lab 4, Page 1

On this page, you create a predicate to check whether one number is divisible by another.

  1. “U2L4-MathLibrary”Start a New Project called U2L4-MathLibrary

  2. Experiment with the () mod () block.

    1. Try various inputs.
    2. Keep the second number constant, and try various inputs for the first number.
    3. Form a hypothesis. What do you notice?

The mod block reports the remainder when the first input is divided by the second. For example, (17) mod (5) reports 2 because when 17 is divided by 5, the remainder is 2. When one number divides another evenly, the remainder is 0. So for example, (15) mod (5) reports 0.

Different programming languages have different ways of handling negative inputs to the mod function. So you won’t see any negative numbers used with mod on the exam.

The mod operator: The expression (17) mod (5) would be written as 
17 MOD 5
on the exam. If you see an expression with variables as input to mod, such as 
a MOD b

, you can assume that a is zero or positive, and b is strictly positive (because you can’t divide by 0).

On the exam, you may see these four arithmetic operators:

+
, 
-
, 
*
, 
/
(plus, minus, times, divide) as well as 
MOD

.

Arithmetic operators are part of most programming languages. (Most text languages use 
*
rather than 
×
for multiplication because 
×

isn’t on most keyboards, and because it looks too much like the letter x.)

Order of operations: In a block language, the nesting of blocks determines the order of operations. For example, in 3 × (5 + 4) you can see that the + block is an input to the × block, so the expression means 3×(5+4). Similarly, (3 × 5) + 4 means (3×5)+4. In Snap!, it’s as if there are parentheses around every operation. But in text languages, you can write

3 * 4 + 5

without parentheses, so they need the rules you learn in math class (multiplication before addition, and so on). The mod operator is like multiplication and division; it happens before addition and subtraction. So for example,

7 + 5 MOD 2 - 6

means

7 + 1 - 6

, which is, of course, 2.

    In a later lab, you can use your even? block to draw a brick wall because the even and odd numbered rows are different.
    Sample image of brick wall

  1. Use mod to build a is () divisible by () ? predicate that tests for divisibility.
    is (15) divisible by (3) ? reporting true is (15) divisible by (6) ? reporting false
  2. Use this divisible by? predicate to build a predicate that tests whether its input is even (divisible by 2).
    even? (-22) reporting true even? (7) reporting false
  3. Save your work

photo of Katherine Johnson

Katherine Johnson (1918–2020) was an aerospace technologist with a Ph.D. in mathematics who worked for NASA calculating the motion of spacecraft. Johnson, originally hired as a human computer, verified the calculations of digital computers, helped calculate the trajectory of Apollo 11 (the first time humans walked on the Moon), worked on plans for a mission to Mars, and encouraged students to pursue careers in science, technology, engineering, and mathematics.

NASA’s memorial video: “Katherine Johnson: An American Hero”

AAP-2.H.2

The procedures

move()

and

turn_clockwise()

aren’t built in to the AP’s language so they are written in lower case like other programmer-defined procedures.

The conditional expression 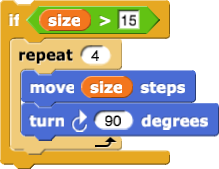if (size > 15) {repeat (4) {move (size) steps, turn clockwise (90) degrees}} would be written as

IF(size > 15)
{
REPEAT 4 TIMES
{
move(size)
turn_clockwise(90)
}
}

or 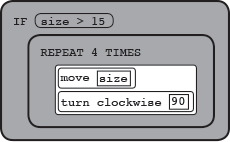IF(size > 15) { REPEAT 4 TIMES { move(size) turn clockwise(90) } }

As in Snap!, if the condition (size) > 15 is true, the code inside the if statement runs; if the condition is false, the code does not run.

  1. Talk with Your Partner Is it true that (12 MOD 2) > (11 MOD 2)? Explain your reasoning.
  1. Build a predicate that tests whether its input is an integer. You may find round () useful.
    integer? (4) reporting true integer? (4.1) reporting false

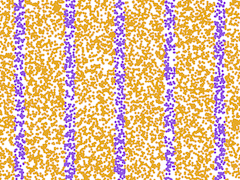
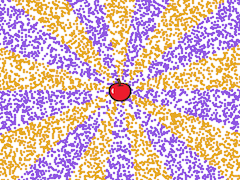
Open your U2L3-Dots project, and save it again as U2L4-DotsTIF. Remind yourself about how the pictures are determined by the Boolean expression used.

  1. Invent Boolean expressions for these pictures:

    1. The stage is almost entirely orange, except for five thin vertical purple stripes evenly spaced.
    2. A checkerboard pattern or purple and orange. Around the x axis are five squares, with purple at the left and right edges and at the center. Around the y axis, there are three full squares and two partial squares at the edges; the partial squares and the center square are purple, and the remaining two squares are orange. The two colors alternate over the entire area like a checkerboard.
    3. A checkerboard like ii, except that in each row the squares alternate two orange, one purple. So the top (partial) row is orange, purple, orange, orange, purple. The second row is purple, orange, orange, purple, orange. The middle row is orange, orange, purple, orange, orange. The fourth row is orange, purple, orange, orange, purple. And the bottom partial row is purple, orange, orange, purple, orange.
    4. There's an apple at the center. Radiating out from the center are 18 wedges, alternating orange and purple in color.
    5. There's an apple at the center. Behind the apple is a small orange circle. Then comes a small purple circular band around the orange circle. Then a small orange circular band, and so on working outward.
    6. Tough StuffImagine a line going straight down from an apple in the center of the stage. Also imagine a spiral that starts at the origin and spirals outward clockwise, through a little bit of the third quadrant, then the second quadrant, and finally hitting the right edge of the stage in the first quadrant. The area above and to the left of the line and spiral is purple; the area below and to the right is orange.

    Click for a hint.

    Some of these include expressions of the form ((round (() / 20)) mod 2) with something like x position in the empty input slot, and maybe different numbers in place of 20 and 2.