Page 3: More Mathematical Reporters

Unit 2, Lab 4, Page 3

In this project, you will create mathematical blocks that combine several numbers, such as a sum block, which combines two numbers using addition:

1. Open your U2L4-MathLibrary project if it isn’t open already.
2. Build blocks for maximum (reporting the larger of two input numbers) and minimum (reporting the smaller of two input numbers):
   

The block takes two inputs: a list and an operation with two inputs, and it reports the result of combining all the elements in the input list using the input operation. For example, the expression below reports: 0 + 1 + 2.

You choose the operation, and combine performs that operation by combining all the items in the input list and then reports the result.

Notice that the function used to combine the list items always has two blank input slots. The keep block only needs one blank in its input function, but with combine, two are required.

Combine is a higher-order function; it is a function that takes a function as input. You’ve seen another higher-order function already: keep (in Unit 2 Lab 3).

Unlike keep, the combine function is only used with a few input functions. Which functions?

Combine is mostly used with only these functions:



and the and blocks you’ve just written yourself.

Why so few?

The function has to be associative, meaning that it can’t matter what order you group the items in. For example, addition is associative: (7 + 8) + 1 is the same as 7 + (8 + 1) (work it out yourself), but subtraction is not: (7 − 8) − 1 is different from 7 − (8 − 1). So expressions like would be ambiguous.

3. Use combine to build maximum of list and minimum of list.
   
4. Create a sum of list block that reports the sum of the items of a list.
   

5. Create an average of list block that calculates the average of the items in a list:
   

   Hint about average of list

   First think: how do you calculate an average? Then think: what blocks could help you do that in Snap!?

AAP-2.M.2, AAP-2.O.4

Average of list and sum of list are procedures that you’ll need repeatedly, so after a while, you just know how to write them, or you’ll put them in a library, and you won’t have to reinvent them each time. Finding the maximum or minimum value in a list and checking for divisibility are also commonly needed algorithms.

AAP-3.C.2

You saw the procedure definition for a command in Unit 1 Lab 3 Page 4: Modify Your Pinwheel.

The definition for a reporter looks much like the definition for a command except that it includes an

RETURN

(like report). For example, this definition

In many languages (including Snap!) variables must be declared in some way (in Snap!, you can click the “Make a variable” button or use the script variables block). But the AP’s language doesn’t include variable declarations, so you won’t see them on the exam.

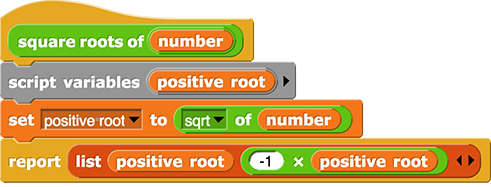
would be written as

PROCEDURE squareRoots(number)
{
positiveRoot ← sqrt(number)
RETURN([positiveRoot, -1 * positiveRoot])
}

or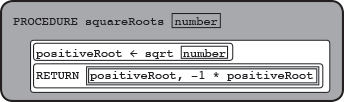

As with report in Snap!, when a

RETURN

statement is executed, the flow of control returns to the place in your code where the procedure was called, and the procedure returns the value of the expression inside the

RETURN

command or report block.

Also, the procedure

sqrt

isn’t built in to the AP’s language so it is written in lower case like other programmer-defined procedures.

AAP-2.H.3

The conditional expression would be written as

IF(a > b)
{
RETURN(true)
}
ELSE
{
RETURN(a = b)
}

or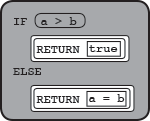

As in Snap!, if the condition

a > b

is true, the code in first block of statements runs; if it is false, the code in second block of statements runs.

1. The greatest common divisor of two integers is the largest positive integer that is a divisor (a factor) of both integers.

   Develop a greatest common divisor block. (Use your block.)
   

   Hint about building greatest common divisor

   You may find it useful to use maximum of list as well as divisors and also to build an intersection block that takes two lists as input and reports all of the items that are on both lists.
   
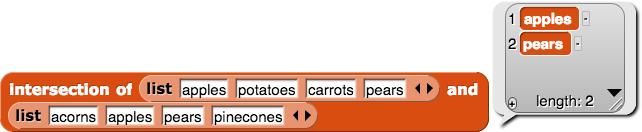
   More detailed hints about greatest common divisor

   In order to find the greatest common divisor of two numbers you will need to find:

   1. The divisors of each input number
   2. The numbers that are divisors of both input numbers
   3. The greatest number that is a divisor of both input numbers