Curve Stitching

Unit 3 Optional Project

PG: I’m glad this now has references to the extensions (and is no longer called Astrid). I like the idea of turtlifying it, though only the hint directs students away from a turtle solution. Using the method of locating the points by algorithm, storing them, then using that list of coordinates will be simpler than pure turtle, possibly even for the cardioid and other such envelopes inside a circle). I’d be inclined to have it start with just the animated image, and another one, a bit slower, animating the cardioid development in a circle (one end moves a step at a time, the other end two steps for cardioid), letting kids figure out what generating rule is involved. It’s just personal taste, but I find “With your partner discuss” to be such a lame schoolish Micky Mouse instruction—no real setting tells us to discuss with our partner. And what business, in an optional project do we have saying “develop an algorithm and then use abstraction”? What sense does it make for us to say how to do what students don’t have to do at all? With the slowly developing image (the current animation is just fine) students should have enough information to invent, if they like.

BH: See the red boxes.

MF: Needs rewrites

Why do this? To give the students a chance to apply their skills of developing algorithms and using abstractions in the context of a visual arts project. To motivate students with interest in arts and to give them an opportunity to synthesize their artistic skills with their knowledge of algorithms and coding.
Why here? At this point in the curriculum the students know enough to be able to complete a computational visual art project with minimal hand-holding.

In this project, you will create a mathematical art design and explore its variations. (Click the picture to see an animation.)

This design uses straight lines to make shapes that look curved and is sometimes sewn with thread or drawn on paper. Here are some examples of and variations on this design made with string, computers, pencils on paper, and even pencils glued together:

• Making Patterns: Pushing the Envelope
• Create Parabolic Curves Using Straight Lines

1. With your partner discuss how to make this design. Develop an algorithm that will generate the first quadrant of the design and then use abstraction to extend the design to the other quadrants.

2. Write a Snap! program to generate the design.

   Mary and Brian want to rewrite this page so that it’s not using fixed coordinates but is “turtly.” –MF, 9/7/18

   Click for a hint about setting up the design.

   Below is a partial table of coordinates for the first quadrant of the design, showing which points on the y-axis are joined to which points on the x-axis.
   

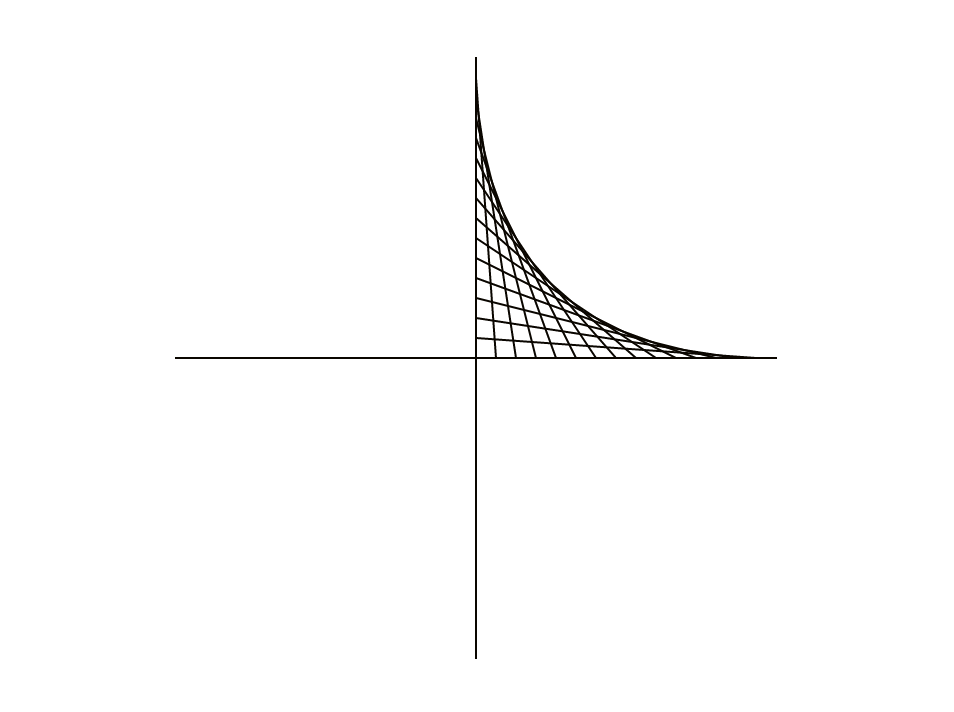
   31b8e172-b470-440e-83d8-e6b185028602:dAB5AHAAZQA6AE8AQQBCAGwAQQBHAFkAQQBOAFEAQgBoAEEARABjAEEATgB3AEEAeQBBAEMAMABBAFoAQQBCAGsAQQBEAFkAQQBNAHcAQQB0AEEARABRAEEATgBnAEEAeQBBAEQASQBBAEwAUQBBADQAQQBEAFEAQQBZAGcAQgBtAEEAQwAwAEEAWQBRAEIAbQBBAEQARQBBAE8AUQBBADUAQQBEAFUAQQBZAFEAQQB4AEEARwBJAEEATQBnAEIAaQBBAEQAawBBAAoAcABvAHMAaQB0AGkAbwBuADoATgBBAEEAeABBAEQAawBBAE8AQQBBAD0ACgBwAHIAZQBmAGkAeAA6AAoAcwBvAHUAcgBjAGUAOgBQAEEAQgAwAEEARwBFAEEAWQBnAEIAcwBBAEcAVQBBAEkAQQBCAGoAQQBHAHcAQQBZAFEAQgB6AEEASABNAEEAUABRAEEAaQBBAEcASQBBAGIAdwBCAHkAQQBHAFEAQQBaAFEAQgB5AEEARwBVAEEAWgBBAEEAaQBBAEMAQQBBAGMAdwBCADAAQQBIAGsAQQBiAEEAQgBsAEEARAAwAEEASQBnAEIAdABBAEcARQBBAGMAZwBCAG4AQQBHAGsAQQBiAGcAQQB0AEEARwB3AEEAWgBRAEIAbQBBAEgAUQBBAE8AZwBBAGcAQQBEAEUAQQBNAEEAQQBsAEEARABzAEEASQBnAEEAZwBBAEgATQBBAGQAUQBCAHQAQQBHADAAQQBZAFEAQgB5AEEASABrAEEAUABRAEEAaQBBAEgATQBBAGQAUQBCAG4AQQBHAGMAQQBaAFEAQgB6AEEASABRAEEAWgBRAEIAawBBAEMAQQBBAGMAQQBCAHYAQQBHAGsAQQBiAGcAQgAwAEEASABNAEEASQBBAEIAbQBBAEcAOABBAGMAZwBBAGcAQQBHAFEAQQBaAFEAQgB6AEEARwBrAEEAWgB3AEIAdQBBAEMASQBBAFAAZwBBAEsAQQBEAHcAQQBkAEEAQgB5AEEARAA0AEEAQwBnAEEAOABBAEgAUQBBAGEAQQBBAGcAQQBIAE0AQQBZAHcAQgB2AEEASABBAEEAWgBRAEEAOQBBAEMASQBBAFkAdwBCAHYAQQBHAHcAQQBJAGcAQQBnAEEASABNAEEAZABBAEIANQBBAEcAdwBBAFoAUQBBADkAQQBDAEkAQQBkAHcAQgBvAEEARwBrAEEAZABBAEIAbABBAEMAMABBAGMAdwBCAHcAQQBHAEUAQQBZAHcAQgBsAEEARABvAEEASQBBAEIAdQBBAEcAOABBAGQAdwBCAHkAQQBHAEUAQQBjAEEAQQA3AEEAQwBJAEEAUABnAEIARwBBAEgASQBBAGIAdwBCAHQAQQBDAEEAQQBLAEEAQgA1AEEAQwAwAEEAWQBRAEIANABBAEcAawBBAGMAdwBBAHAAQQBEAHcAQQBMAHcAQgAwAEEARwBnAEEAUABnAEEASwBBAEQAdwBBAGQAQQBCAG8AQQBDAEEAQQBjAHcAQgBqAEEARwA4AEEAYwBBAEIAbABBAEQAMABBAEkAZwBCAGoAQQBHADgAQQBiAEEAQQBpAEEAQwBBAEEAYwB3AEIAMABBAEgAawBBAGIAQQBCAGwAQQBEADAAQQBJAGcAQgAzAEEARwBnAEEAYQBRAEIAMABBAEcAVQBBAEwAUQBCAHoAQQBIAEEAQQBZAFEAQgBqAEEARwBVAEEATwBnAEEAZwBBAEcANABBAGIAdwBCADMAQQBIAEkAQQBZAFEAQgB3AEEARABzAEEASQBnAEEAKwBBAEYAUQBBAGIAdwBBAGcAQQBDAGcAQQBlAEEAQQB0AEEARwBFAEEAZQBBAEIAcABBAEgATQBBAEsAUQBBADgAQQBDADgAQQBkAEEAQgBvAEEARAA0AEEAQwBnAEEAOABBAEMAOABBAGQAQQBCAHkAQQBEADQAQQBDAGcAQQA4AEEASABRAEEAYwBnAEEAKwBBAEEAbwBBAFAAQQBCADAAQQBHAFEAQQBQAGcAQQBvAEEARABBAEEATABBAEEAZwBBAEQARQBBAE4AUQBBAHcAQQBDAGsAQQBQAEEAQQB2AEEASABRAEEAWgBBAEEAKwBBAEEAbwBBAFAAQQBCADAAQQBHAFEAQQBQAGcAQQBvAEEARABBAEEATABBAEEAZwBBAEQAQQBBAEsAUQBBADgAQQBDADgAQQBkAEEAQgBrAEEARAA0AEEAQwBnAEEAOABBAEMAOABBAGQAQQBCAHkAQQBEADQAQQBDAGcAQQA4AEEASABRAEEAYwBnAEEAKwBBAEEAbwBBAFAAQQBCADAAQQBHAFEAQQBQAGcAQQBvAEEARABBAEEATABBAEEAZwBBAEQARQBBAE4AQQBBAHcAQQBDAGsAQQBQAEEAQQB2AEEASABRAEEAWgBBAEEAKwBBAEEAbwBBAFAAQQBCADAAQQBHAFEAQQBQAGcAQQBvAEEARABFAEEATQBBAEEAcwBBAEMAQQBBAE0AQQBBAHAAQQBEAHcAQQBMAHcAQgAwAEEARwBRAEEAUABnAEEASwBBAEQAdwBBAEwAdwBCADAAQQBIAEkAQQBQAGcAQQBLAEEARAB3AEEAZABBAEIAeQBBAEQANABBAEMAZwBBADgAQQBIAFEAQQBaAEEAQQArAEEAQwBnAEEATQBBAEEAcwBBAEMAQQBBAE0AUQBBAHoAQQBEAEEAQQBLAFEAQQA4AEEAQwA4AEEAZABBAEIAawBBAEQANABBAEMAZwBBADgAQQBIAFEAQQBaAEEAQQArAEEAQwBnAEEATQBnAEEAdwBBAEMAdwBBAEkAQQBBAHcAQQBDAGsAQQBQAEEAQQB2AEEASABRAEEAWgBBAEEAKwBBAEEAbwBBAFAAQQBBAHYAQQBIAFEAQQBjAGcAQQArAEEAQQBvAEEAUABBAEIAMABBAEgASQBBAFAAZwBBAEsAQQBEAHcAQQBkAEEAQgBrAEEARAA0AEEATABnAEEAdQBBAEMANABBAFAAQQBBAHYAQQBIAFEAQQBaAEEAQQArAEEAQQBvAEEAUABBAEIAMABBAEcAUQBBAFAAZwBBAHUAQQBDADQAQQBMAGcAQQA4AEEAQwA4AEEAZABBAEIAawBBAEQANABBAEMAZwBBADgAQQBDADgAQQBkAEEAQgB5AEEARAA0AEEAQwBnAEEAOABBAEgAUQBBAGMAZwBBACsAQQBBAG8AQQBQAEEAQgAwAEEARwBRAEEAUABnAEEAbwBBAEQAQQBBAEwAQQBBAGcAQQBEAEkAQQBNAEEAQQBwAEEARAB3AEEATAB3AEIAMABBAEcAUQBBAFAAZwBBAEsAQQBEAHcAQQBkAEEAQgBrAEEARAA0AEEASwBBAEEAeABBAEQATQBBAE0AQQBBAHMAQQBDAEEAQQBNAEEAQQBwAEEARAB3AEEATAB3AEIAMABBAEcAUQBBAFAAZwBBAEsAQQBEAHcAQQBMAHcAQgAwAEEASABJAEEAUABnAEEASwBBAEQAdwBBAGQAQQBCAHkAQQBEADQAQQBDAGcAQQA4AEEASABRAEEAWgBBAEEAKwBBAEMAZwBBAE0AQQBBAHMAQQBDAEEAQQBNAFEAQQB3AEEAQwBrAEEAUABBAEEAdgBBAEgAUQBBAFoAQQBBACsAQQBBAG8AQQBQAEEAQgAwAEEARwBRAEEAUABnAEEAbwBBAEQARQBBAE4AQQBBAHcAQQBDAHcAQQBJAEEAQQB3AEEAQwBrAEEAUABBAEEAdgBBAEgAUQBBAFoAQQBBACsAQQBBAG8AQQBQAEEAQQB2AEEASABRAEEAYwBnAEEAKwBBAEEAbwBBAFAAQQBCADAAQQBIAEkAQQBQAGcAQQBLAEEARAB3AEEAZABBAEIAawBBAEQANABBAEsAQQBBAHcAQQBDAHcAQQBJAEEAQQB3AEEAQwBrAEEAUABBAEEAdgBBAEgAUQBBAFoAQQBBACsAQQBBAG8AQQBQAEEAQgAwAEEARwBRAEEAUABnAEEAbwBBAEQARQBBAE4AUQBBAHcAQQBDAHcAQQBJAEEAQQB3AEEAQwBrAEEAUABBAEEAdgBBAEgAUQBBAFoAQQBBACsAQQBBAG8AQQBQAEEAQQB2AEEASABRAEEAYwBnAEEAKwBBAEEAbwBBAFAAQQBBAHYAQQBIAFEAQQBZAFEAQgBpAEEARwB3AEEAWgBRAEEAKwBBAEEAPQA9AAoAcwB1AGYAZgBpAHgAOgA=:31b8e172-b470-440e-83d8-e6b185028602

   Click for a suggestion about how to start in Snap!

   There are many possible approaches to this problem. One approach could use the for block:
   

3. Using the same principles, create a surrounding frame for your design.
   

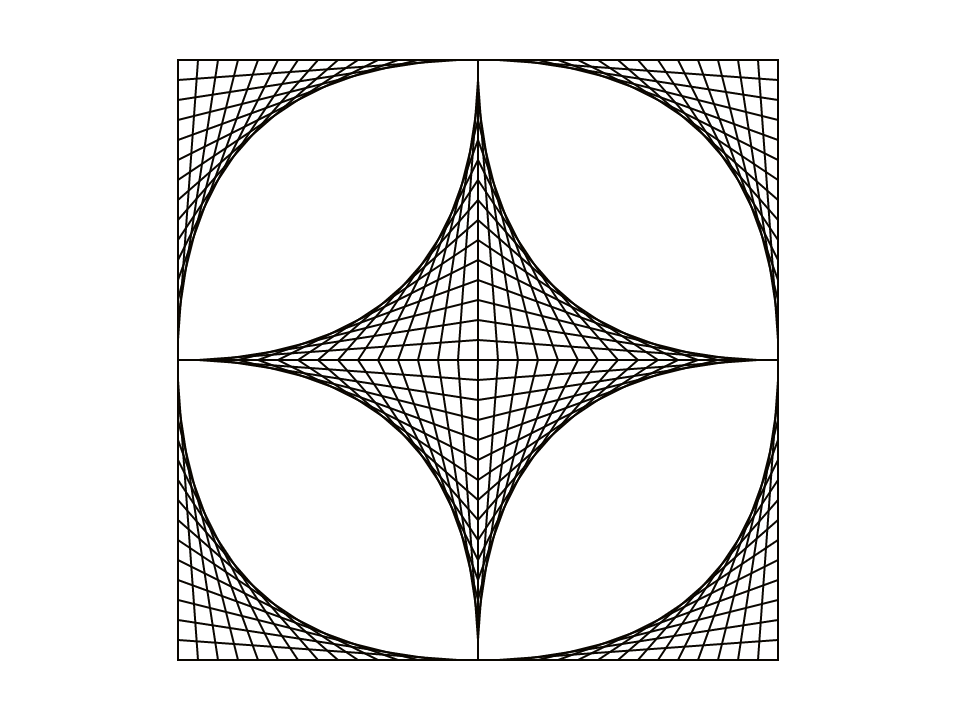
   Both the original curve and the frame are made of four quarter-pictures.

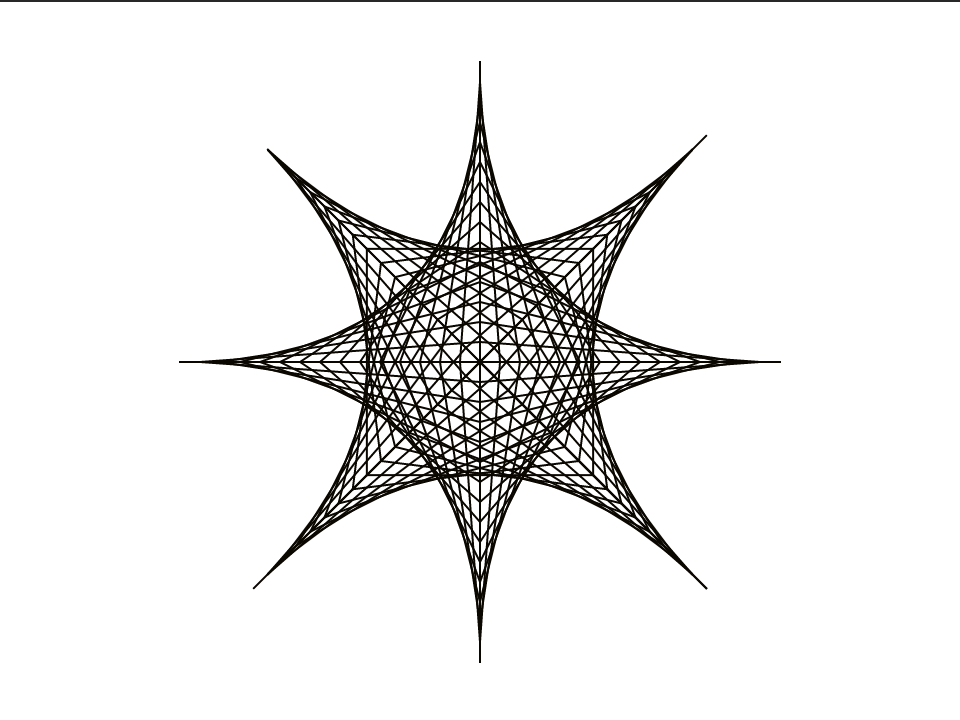
1. Add another copy of the design slanted at 45° as shown below.
   

   Want a mathematical hint?

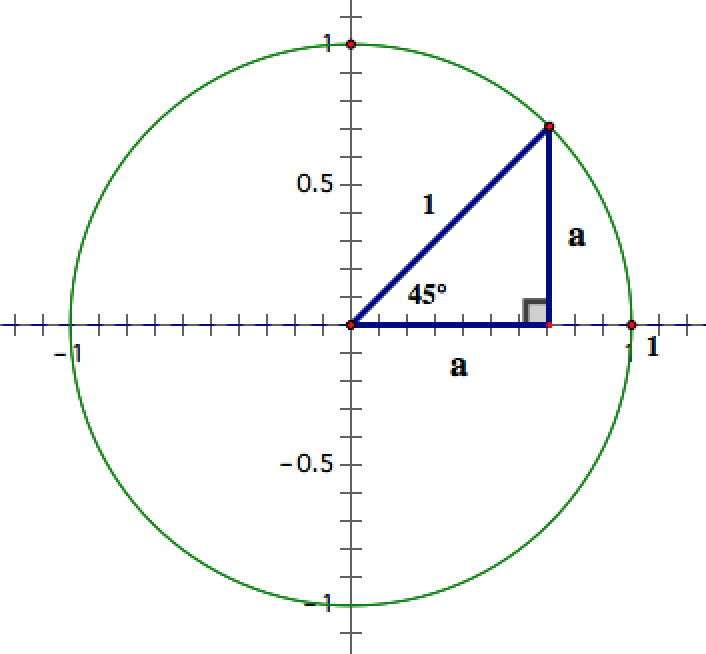
   You could use the Pythagorean Theorem:
   

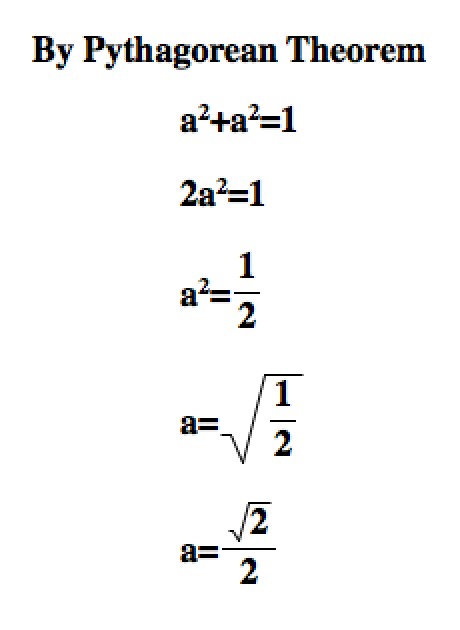
2. Here are some more variations that employ color and more complex geometric arrangements. Create these and your own variations in Snap!.
   

3. Use what you know about creating animations in Snap! to produce an animation based on this design. To allow for dynamic movements such as rotations, you will need to devise a completely different way of creating your design than using fixed coordinates.
   

   Want to see an example?

   This animation explores the artistic concept of “negative space” by using a grid of rotating copies of the design. How would you revise your program to generate animations like this?