Page 2: An Undecidable Problem

Unit 5, Lab 4, Page 2

PG: This is a lovely piece of logic, well written. I’d love to keep it (and see if we can simplify writing even further), but reasoning by contradiction is notoriously hard in all contexts (though, perhaps, page 1 sets it up well enough?) and it isn’t obvious that doing it in a programming context would be easier. In fact, the unfamiliarity and extra layer of technicality might make it harder. Do we have any feedback? All this said, CB insists on “teaching this,” so the question is how we can make more than an empty factoid out of it. I like our approach. Does it work?

BH: But FYTD 1c is kinda TIFfy. And, I think Church actually proved it before Turing, but we should check. And, bring back his picture!

MF: I want to review this page just because the idea deserves it

On this page, you will consider a problem that can’t have an answer.

By this point in the course, you’ve experienced the frustration of debugging a program. It would be great if there were a general-purpose debugging program that could read any code and determine if there were bugs. Unfortunately, we can use proof by contradiction (as Alphie, Betsy, and Gamal did on the previous page) to prove that this can’t be done.

First, we’ll assume that it’s possible to write a function to determine if there are infinite loops in a program (situations in which a function runs forever without reporting a value). Then, we’ll use that function in a program especially designed to create a contradiction (a logical incompatibility) to prove that the assumption is wrong—no general-purpose debugging program can exist. “Does this program have bugs” is an undecidable problem; no algorithm can ever be constructed that always solves it correctly for every program.

An infinite loop is a sequence of computer instructions that repeats forever.

An unsolvable problem is one for which no algorithm can ever be written to find the solution.

An undecidable problem is one for which no algorithm can ever be written that will always give a correct true/false decision for every input value. Undecidable problems are a subcategory of unsolvable problems that include only problems that should have a yes/no answer (such as: does my code have a bug?).

Assuming That a Halts? Function Exists

Making the Assumption

We can’t show the code inside halts?; we are proving that it can’t be written at all, no matter what code implements it.

First, we assume there exists a function called halts? that determines whether a given reporter will report a value in a finite time. (If so, we say that the reporter halts.) It takes two inputs: a function and an input value for that function. It reports true if the function would report a value when given that input; it reports false if the function would run forever (in an infinite loop).

For example, the function round will not run forever when given the input 7.5; it will report 8.

The gray ring around the input function means that the halts? code will treat the input function as data instead of running it.

because reports a value.

On the other hand, imagine we had a function that will get stuck in an infinite loop when given the input foo; it would never report (never halt).

because loops infinitely.

Reviewing the Plan for the Proof

We’ll use proof by contradiction to show that the following question can’t be answered in general:

Will a certain computer program, given a certain input, report a result in a finite amount of time?

The “computer program” is the first input to halts?. The “given input” is the second input to halts?. And what halts? reports is either true or false: yes the “computer program” will halt or no it won’t.

Note that halts? itself must always report a result, even if the program it’s testing doesn’t. This is because we are assuming (an assumption we’ll show is false) that halts? always works—that it always reports an answer.

We can answer this question for some specific functions, but we are trying to determine whether we can devise a general test that will tell us whether any particular function will report a value for any specific input.

What does it mean to answer the question for specific functions?

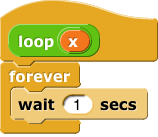
The “in general” part is important. Of course we can answer the question for certain particular programs. This one halts (reports a value) for any input:

This one never halts for any input:

And this one halts sometimes—for any input except 87:

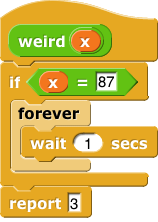
Recall: the question is whether we can devise a test that will tell us whether any particular function will report a value for any specific input.

1. 

   1. Describe the process of proof by contradiction.
   2. Describe what the halts? function does.
   3. Describe how you are going use the halts? function in this proof by contradiction process.

Showing How This Creates a Contradiction

Constructing a Program For Which Halts? Won’t Work

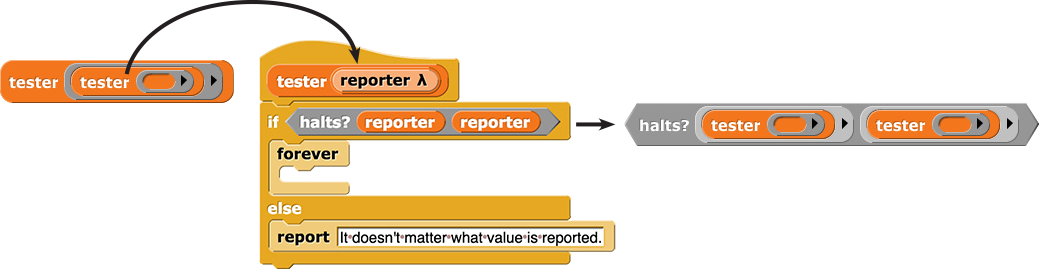
To prove there can be no such function, we need to create a contradiction. We need to show that there has to be at least one function and one input to that function for which halts? fails to work the way we assumed it does. So, we can make up a block, tester, specifically for the purpose of breaking halts?:

Just like the \# and ⋮ symbols for inputs declared to be numbers or lists, the λ is not part of the input’s name but is a type hint that was created when selecting the reporter input type:


Recall that selecting an input type changes the appearance of the input slot so that it indicates what kind of input is expected. The input slot for tester will have a rounded gray ring to indicate that the input should be a reporter:

The forever block in this script creates an infinite loop. If the tester code ends up in this part of the if statement, it will never report anything. So whether tester itself will halt depends on the output of the halts? predicate in the if statement inside it.

The expression asks what will happen if we call the input function (reporter) with itself as its own input. This is similar to when Betsy made a statement about the statement she was making, when she said, “The statement I’m making right now is false.”

This is challenging. Stick with it! We are creating a contradiction to prove that the halts? function called inside tester can’t exist.

Using Self-Reference to Lead to Contradiction

To make the situation exactly like what Betsy said (“The statement I’m making right now is false.”), we’ll call tester on itself:

Now, the if statement inside the tester block will ask if tester will halt (not run forever) if it’s called with tester as its input. The predicate in the if statement will become halts? (tester) (tester).

I took out class=“ms-4” on this picture so that it’d fit in the window. If you don’t like that, figure out how to shrink the picture without fuzzing it up. -bh
OK, leaving this comment here to remind me for another day. –MF, 2/1/18

So, just as in the examples above,

would mean that returns a value.

would mean that loops infinitely.

Understanding the Contradiction

When we call , we run into the contradiction. To see how, look back at the tester definition:

Showing that the result has to be wrong involves a case analysis like the ones used to solve the logic puzzles on page 1. Consider the two possible cases:

1. If then tester will take the first branch of the if, and so it will loop forever. That means won’t halt, and so halts? gave the wrong answer.
2. If then tester will take the else branch and report “It doesn’t matter what value is reported.” That means will halt, and so halts? is wrong again.

It doesn’t matter what value tester reports, just that it reports some value, but it does matter what value halts? reports.

No matter what halts? reports, it will always disagree with itself in a program like this. This contradiction (this logical impossibility) means that the assumption that it’s possible write halts? has to be wrong. This isn’t just a claim about what will happen in Snap!. The language you use to explore a computational problem can impact the clarity or readability of your code but not whether a solution to a problem exists. Even with advances in quantum computing, we will never be able to create a general-purpose debugging program. This famous example is known as the halting problem, and the fact that the halting problem is not decidable is the Halting Theorem.

2. Go over this whole proof again together. Make sure both you and your partner understand:

   1. Everything from exercise 1 about proof by contradiction, what halts? does, and how halts? is going to be used in the proof
   2. The basics of how the tester function behaves (for any input function)
   3. How calling leads to a contradiction
   4. What that contradiction means in the proof
   5. Whether the Halting problem is an unsolvable problem, an undecidable problem, or both; and why
3. Write a paragraph explaining the difference between an problem that can’t be solved (such as the halting problem) and a problem that takes unreasonable time.

Alan Turing (1912–1954) was a British computer scientist and mathematician. During World War II, he developed a number of critical technologies to decipher encrypted German messages, playing a key role in helping the Allied forces defeat the Nazis. While working at the University of Manchester after the war, he devoted more of his time to the idea of Artificial Intelligence, proposing what is now known as the “Turing Test”. Together with his colleague Alonzo Church, Turing was a founder of theoretical computer science: proving that computers must work regardless of future technology.

He proved that there are well-defined mathematical problems that computers can never solve, no matter how large and fast they get. Tragically, Turing was prosecuted for “indecency” when authorities discovered he was gay, and it is suspected that he commited suicide after being subjected to hormone treatments. He is often considered to be the “father of modern computing.”

Article: Overlooked No More