Page 6: Looping with a Counter

Unit 1, Lab 3, Page 6

On this page, you will use for loops not only to repeat, but also to count the repetitions and then use that counter to draw shapes with repeated patterns:

You’ve seen these ways to repeat a set of commands:

The forever block generates an infinite loop that goes on forever. An infinite loop can sometimes be the result of a bug, but in some interactive programs, you want the program to keep running until stopped by the user.

• repeats the same commands forever. (You used it to make Alonzo keep moving in Unit 1 Lab 1 Page 2: Programming a Game.)

• repeats them a specific number of times. (You used it to draw shapes in Unit 1 Lab 3 Page 1: Exploring Motion.)

: Iteration

Computer scientists describe a repeating program structure as looping, repetition, or iteration.

The code can be repeated forever, a specific number of times (such as when using repeat), or until something specific happens (such as when using repeat until as you’ll see in Lab 5).

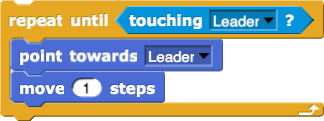
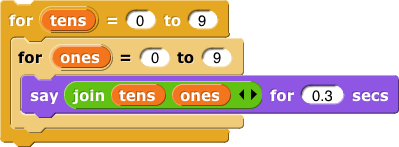
Sometimes the script inside a loop needs to know which time through the loop it’s in (first, second, etc.). You can use to keep track, and you can use its counter (the default name is ) in the repeated script. For example, the for block lets you simplify long scripts like:

to

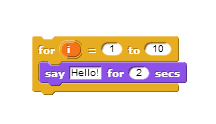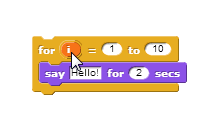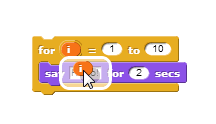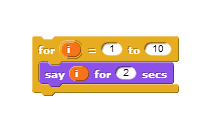
Each time the for block runs the script inside, it changes the value of the counter by 1, beginning with the first input number and ending after the second.

The for block’s default counter name, stands for “index.” You can change this name by clicking it. To use the counter, drag it into the script.

1. Build this script that makes the sprite say the numbers 1 through 10.
   
   1. Then modify it so that the sprite says 0, 2, 4, 6, 8, … up through 30.
   2. Discuss your solutions with another pair.
2. Experiment with spirals.

1. Build this script and try it out:
   

   This design got the nickname “squiral” because it’s a square spiral.

   
   

2. Make sure you can explain why the squiral spirals outward.
3. Try switching the order of the 100 and the 1 in the for block in the squiral script. What is the result?
4. Try changing the turning angle in the squiral script to other numbers such as 92, 126, etc.
5. Change the inputs to turn and move to get as close as you can get to a smooth spiral:
   

3. “U1L3-Squiral”

4. Open your U1L3-Pinwheel project, and build a nest squares block that uses for and your polygon block to draw nested squares. Give it an input so that it will draw whatever number of squares you specify, with each square larger than the previous:
   

6. Build nest polygons that accepts the number of polygons and the number of sides for the polygons.

7. Build a script that draws 12 regular polygons, each with one more side than the previous one, as shown below.
   

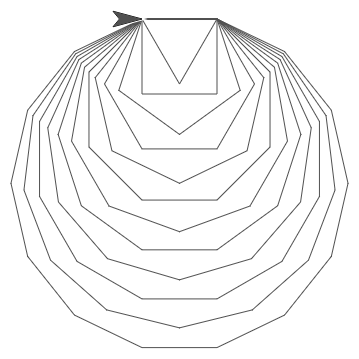
8. Predict what this script will do before you try it:
   

9. Build a script that counts down by 10 from 100 to 0 (that is, 100, 90, 80, etc.).

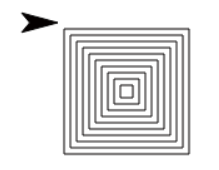
10. Below are two animations that use the pinwheel code with inputs. Find out how to create your own artistic animations.
    
    

    The following code may give you ideas about how to create animations. The warp block allows the drawing of the pinwheel all at once.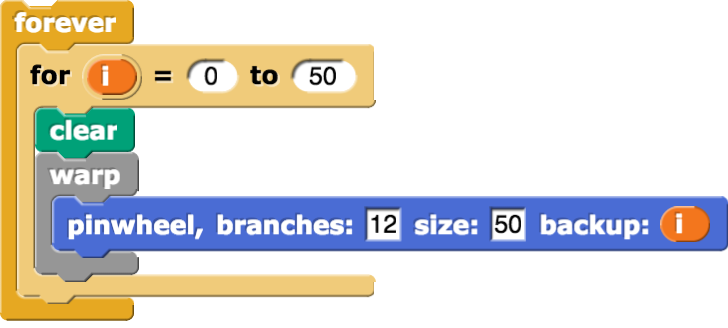

    

11. Make sure your other work has been saved, then
    Experiment with the script. Could you change the sizes or colors to make it more interesting?

                    

1. Find a way to use for to nest squares this way. Build your block with two inputs that let you specify how many squares the design will contain and how much bigger each square will be than the previous one.
   

On the right is a painting by Josef Albers. He was interested in experimenting with variations of color within a “family” of similar colors. Snap! will let you make similar experiments.

2. What is the favorite color of the author of this activity?
3. If you didn’t do the Take It Further activity based on this Kazimir Malevich picture then read it now to learn about Snap! features for solid rectangles and color families.
4. If you haven’t already, do If There Is Time #10, which shows a simple version of this project idea.

5. Okay, now dig in.

   Randomness: The four examples above are different from the actual Albers picture in that they include occasional colors that aren’t from the same family. This can make the pictures more interesting to someone who doesn’t share Albers’s interest in subtle differences in color. (Albers himself, in fact, had more color variation in other pictures of this type.) Too much randomness, though, can make the picture less interesting. Compare the last two examples above; the left one of those two is clearly based on the orange family, with rainbow-neighbors red and yellow, but the right one has violets, greens, oranges, a yellow—too much chaos, maybe. Look back at the Gossip project if you don’t remember how to choose something special once out of six times, or once out of 14 times. Other random choices you can make are the number of squares, how much to shrink the size from one square to the next, and how much to move the corner of the next square horizontally and vertically (the picture is more interesting if those two numbers are different, so the smallest square isn’t exactly in the center).

6. This block is like the squiral, but instead of changing the input to move, it changes the input to turn:
   

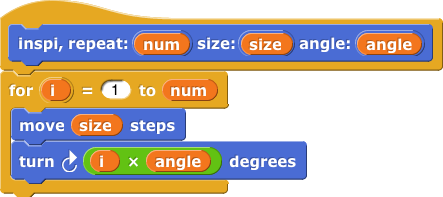
   1. Try sketching what it will draw with an angle of 2.

   2. Then build it, and try each of these tests:
      

      You can stop each test with the stop button when you’re sure nothing new will happen, but don’t decide that too quickly!

      

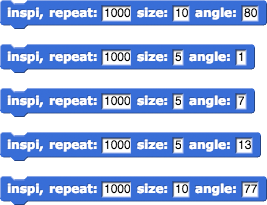
   3. What’s going on? Can you work out a theory to predict anything about the shape it draws for a particular angle input? (Don’t click unless you need a big hint.)

      Hint: Think about divisibility.